-
Innlegg
229 -
Ble med
-
Besøkte siden sist
Innholdstype
Profiler
Forum
Hendelser
Blogger
Om forumet
Innlegg skrevet av duperjulie
-
-
Førsteordens inhomogene differensiallikninger, ubestemte koeffisienters metode
Jeg har følgende difflikning: y'' + 6y' + 18y = 45cos(3t)
Oppgaven ber meg finne den stasjonære løsningen, dvs løsningen når t --> uendelig, og yh blir null)
Jeg har funnet yh (dvs løsningen på y'' + 6y' + 18y = 0) :
yh = e-3t(Acos(3t) + Bsin(3t)).
Så skal jeg inne yp.
Etter tabellen for ubestemte koeffisienters metode, svarer r(t) = 45cos(3t) til at yp = Ccos(3t) + Dsin(3t).
Men er ikke dette allerede en løsning av den homogene versjonen av likningen, og derfor må jeg bruke modifikasjonsregelen, og gange hele yp med t? Dette har de ikke gjort i LF, og bare valgt yp til å være Ccos(3t) + Dsin(3t). Jeg skjønner ikke hvorfor det? Har det noe å gjøre med at jeg skal finne den stasjonære løsningen, og da kan jeg bare se bort ifra yh? Eller har jeg misfotstått, og Ccos(3t) + Dsin(3t) ikke er en løsning av den homogene versjonen?
-
Når det er snakk om vektorfunksjoner, hva er egentlig forskjellen på dr/dt og ds/dt?
Både r(t) og s(t) representerer posisjonen til en partikkel ved tiden t? Eller s representerer kanskje en liten lengde langs kurven?
I boka mi står det at dr/dt = v(t), og at ds/dt = |v(t)|. Men jeg skjønner ikke helt hvorfor det er sånn?
-
Hva vil være den enkleste, billigste og minst risikable måten å kolapse en supermakt som f.eks USA?
word
-
Jeg har oppgitt matrisa M:
1 0 0 0 0
-t 1 0 1 1
0 -t 1 0 1
0 0 -t -1 0
Skal finne ut for hvilke verdier av t det finnes en 5x4-matrise L slik at ML = I (identitetsmatrisa).
L er altså inversen tl M.
Tenkte først å bruke at M har en invers hvis og bare hvis |M| ≠ 0. Men man kan jo ikke finne determinanten til en ikke-kvadratisk matrise?
Noen forslag til hva jeg heller kan gjøre?
-
-
Rotasjon av kjeglesnitt
Når man skal skrive om likninga for et kjeglesnitt slik at man kan skissere den i det roterte planet, har man at den kvadratiske formen til den omformede likninga er gitt ved:
q(x') = λ1(x')2 + λ2(y')2.
Vil ikke da likninga du får avhenge av hvilken egenverdi du velger som λ1, og hvilken du velger som λ2?
Det skal jo ikke ha noe å si, så lenge du konstruerer P slik at rekkefølgen på egenvektorene i P stemmer overens med rekkefølgen på egenverdiene i D?
Edit: Jeg fant det ut selv=) Dette bestemmes ved fortegnet til |P|. Hvis |P| = -1, må man bytte om på kolonnene i P, dvs man bytter på en måte ut hva som er λ1 og hva som er λ2.
-
 1
1
-
-
Aha! Mange takk
-
Vektorrom
Hva betyr notasjonen Rn→ R ?
(Jeg vet at R er de reelle tall, og Rn er et vektorrom med n dimensjoner)
-
Dobbelsjekk fortegnet på lambda2.

Jeg fikk at det var feil fortegn på lamda1 ikke 2'ern
Tusen takk dere=) Man blir litt blind av å sitte for lenge på lesesalen

-
Jeg har et system med to difflikninger.
Koeffisientmatrisa er
(-4/25) (1/25)
(4/25) (-4/25)
(Har skilt hvert element med parentes, fordi det fløyt litt inn i hverandre)
Har funnet egenverdiene: lambda1 = -6/25 og lambda2 = 2/25
Som egenvektor til lambda1 fant jeg (1 2). Men når jeg prøver å finne egenvektor til lambda2, får jeg bare nullvektoren. Det kan jo ikke stemme?
Matrisa jeg skal gausseliminere for å finne lambda2 blir (løser systemet (A -lambda * I)v = 0 )
(-6/25) (1/25)
(4/25) (-6/25)
hvor jeg ender opp med
1 0
0 1
som jo tilsier at x1 = 0 og x2 = 0, og da blir jo egenvektoren 0-vektoren?
Har jeg gjort noe feil underveis?
-
Null stress!Ok=) Takk igjen!Eksamen i matte3 som står for døren?

Stemmer=)
-
Så lenge egenvektoren v oppfyller (gitt at matrisen du startet med heter A):Hvorfor kan jeg ikke bare bruke vektorene [1 0 0 0] og [0 1 0 0] som basis for egenrommet korr. til lamda=1 ? Disse er vel lineært uavhengige? Jeg mener å huske at det er slik man finner basis for vanlige nullrom?
- A*v = lambda*v (egenverdiligningen)
- v er lineært uavhengig av alle andre egenvektorer
skal det være et gyldig valg.
Du kan jo bare sjekke om det stemmer for [1 0 0 0] og [0 1 0 0].

Ok=) Takk igjen!
- A*v = lambda*v (egenverdiligningen)
-
Jeg må finne røttene til likningen
(3-x)(-2-x)(1-x) + 6(1-x) =0
(eventuelt x3 + 2x2 + x = 0).
De to er ikke ekvivalente. Hvilken mener du?
Oi, det skulle stått x3 - 2x2 + x = 0, da er de ekvivalente.
-
Du har ikke noe konstantledd i ligningen din, så x=0 er en løsning. Så deler du med x, og står igjen med x2 + 2x + 1 = 0, som du kan bruke andregradsformelen på. Dette har ikke noe med "Factor theorem of algebra" som du nevner, men metoden funker.
Jah! Selvfølgelig! Tusen takk=)
-
Jeg må finne røttene til likningen
(3-x)(-2-x)(1-x) + 6(1-x) =0
(eventuelt x3 + 2x2 + x = 0).
Hvordan kan jeg gjøre det? Hadde jeg ikke hatt + 6(1-x) hadde det vært lett, men det leddet ødelegger. Har prøvd med forskellige andre faktoriseringer også, men kommer ingen vei.
Boka mi nevner "the factor theorem of algebra", men forklarer ikke hvordan det gjøres.
-
Tusen tusen takk! Det var veldig oppklarende!
Bare et lite spørsmål: Hvorfor kan jeg ikke bare bruke vektorene [1 0 0 0] og [0 1 0 0] som basis for egenrommet korr. til lamda=1 ? Disse er vel lineært uavhengige? Jeg mener å huske at det er slik man finner basis for vanlige nullrom?
-
Hint: Lineære kombinasjoner.
Jeg skjønner fortsatt ikke helt. Jeg ser jo at to av egenvektorene som er oppgitt i løsningsforslaget er lineærkombinasjoner av de opprinnelige vektorene jeg fant, men jeg ser ikke helt logikken.
Er det en regel at når man har to identiske egenverdier, så skal man tilegne de to forskjellige egenvektorer (for eksempel ved å benytte seg av lineærkombinasjoner)? Alle egenverdier har jo uendelig mange egenvektorer med samme retning, så det er vel ikke nødvendig å gjøre det?
-
Matriser og egenvektorer.
Jeg har en oppgave hvor jeg skal finne egenverdiene og de tilhørende egenvektorene til en gitt matrise, pluss finne basis for egenrommene.
Jeg har funnet følgende egenverdier til en gitt 4x4-matrise: λ1 = λ2 = 1, og λ3 = λ4 = 2.
Ved å løse (A - λI)v = 0 for λ = 1 og (A - λI)u = 0 for λ = 2, har jeg fått at v = t[1 0 0 0] + s[0 1 0 0], og at
u = t[1 1 1 0] + s[0 0 0 1].
Det jeg ikke helt skjønner nå, er hva som blir korresponderende egenvektorer til hvilke egenverdier og sånn.
Jeg trodde det var slik:
v er korrepsonderende egenvektor til både λ1 og λ2, siden disse egenverdiene er like, og at u er korresponderende egenvektor til både λ3 og λ4.
Og at basis for korresponderende egenrom til λ1 og λ2 er v1 = [1 0 0 0] og
v2 = [0 1 0 0], basis for korresponderende egenrom til λ3 og λ4 er u1 = [1 1 1 0] og u2 = [0 0 0 1]
Men løsningsforslaget sier dette:
Etter litt regning får vi at λ = 1 gir løsningen v = t(1,0,0,0) + s(0,1,0,0),s,t ≠ 0 siden x3 og x4 må være 0, og x1 og x2 er frie variable, mens λ = 2 gir u = t(1,1,1,0)+ s(0,0,0,1),s,t ≠ 0 siden x3 og x4 er frie variable og x1 = x2 = x3. (Så langt er jeg enig)
Vi ser at egenrommet tilhørende λ1 = λ2 = 1 har dimensjon 2, og v1 = (1,0,0,0),v2 = (1, 1, 0, 0) vil utgjøre en basis for dette rommet. Egenrommet tilhørende λ3 = λ4 = 2 har også dimensjon 2, og v3 = (1, 1, 1, 0), v4 = (1, 1, 1, 1) vil utgjøre en basis for dette rommet.
Løsningen blir altså λ1 = 1,v1 = (1,0,0,0); λ2 = 1,v2 = (1,1,0,0); λ3 = 2,v3 = (1,1,1,0); λ4 = 2,v4 = (1,1,1,1)
Hvorfor tilegnes her én egenvektor til hver egenverdi, og hvordan kommer man frem til dette? Ser også at disse er brukt som basis, og ikke løsningene på (A - λI)v = 0.
Jeg må ha misforstått konseptet tror jeg. Er det noen som kan være så inderlig snille å forklare? (A)
-
Flateintegral
Jeg skal parametrisere toppen av en elliptisk paraboloide gitt ved z = 2 - x2 - , avgrenset av kjeglen
z = sqrt(x2 + y2).
Hvordan gjør jeg det?
Har funnet parametrisering av ellipsoiden: r(r,theta) = [rcos(theta), rsin(theta),2-r2].
Og parametrisering av kjeglen: r(r,theta) = [rcos(theta), rsin(theta),r]
Ser at disse er like for r=1. Men hvilken skal jeg bruke for å få den riktige flaten, og hvordan?
-
La a være en vektor.
Hvorfor gjelder aTa = a*a ?
-
(Beklager hvis dette er postet feil, men fysikk var det nærmeste jeg kom)
Problemet angår likestrømsmaskin, nærmere bestemt shuntmaskin.
Jeg skal regne på en shuntmaskin, men har bare fått masse begreper og ting og tang, uten at det står noe sted hva dette er for noe. Så jeg lurer på om noen kan forklare meg hva følgende er:
- Magnetiseringsvikling
- Ankervikling
- Klemmespenning
- Børster
Noen som kan forklare meg hva det er?
-
Hvis x og y skal gå fra 0 til uendelig så er integrasjonsområdet første kvadrant. For å dekke første kvadrant må theta gå fra 0 til pi/2 og r, som du sier, fra 0 til uendelig.
Aha, ja det virker jo logisk. Tusen takk=)
-
Jeg har et uegentlig dobbeltintegral som jeg skal konvertere til et polart integral. Selve uttrykket er greit å konvertere, men jeg er litt usikker på grensene.
funkjsonsuttrykket er: 1/((1 + x2 + y2)2)
eller altså: 1/((1 + r2)2)
Grensene er : x fra 0 til uendelig og y fra 0 til uendelig.
Hvordan finner jeg grensene for r og tetta?
Er det riktig at r også går mot uendelig, fordi r2 = x2 + y2?
-
Jeg har oppgitt et plan, x - 2y + 5z = 0. Hvordan kan jeg finne ut om vektorene i dette planet danner en basis for R3 ?
Se om en vilkårlig vektor i R3 er en lineær kombinasjon av vektorene i planet.
Finn ut for hvilken x K(x) - I(x) er størst. Dvs. deriver uttrykket og finn nullpunktet av det uttrykket.
Edit: Oi, ja. I(x) - K(x) selvfølgelig. Så feil av funksjonene. Selv om begge deler gir rett svar er det nok intuitivt best slik.
Men hvordan veit jeg hvilke vektorer jeg skal velge? Er jo uendelig mange vektorer i det planet



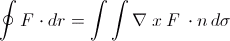
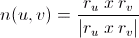
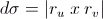
Den enorme matteassistansetråden
i Skole og leksehjelp
Skrevet
Jeg har et enormt uttrykk som inneholder mange ledd med cos((3*n*pi)/4) og cos((n*pi)/4). Er det mulighet for å uttrykke den ene vha den andre på en eller annen måte? Hvis ikke sitter jeg bom fast:S